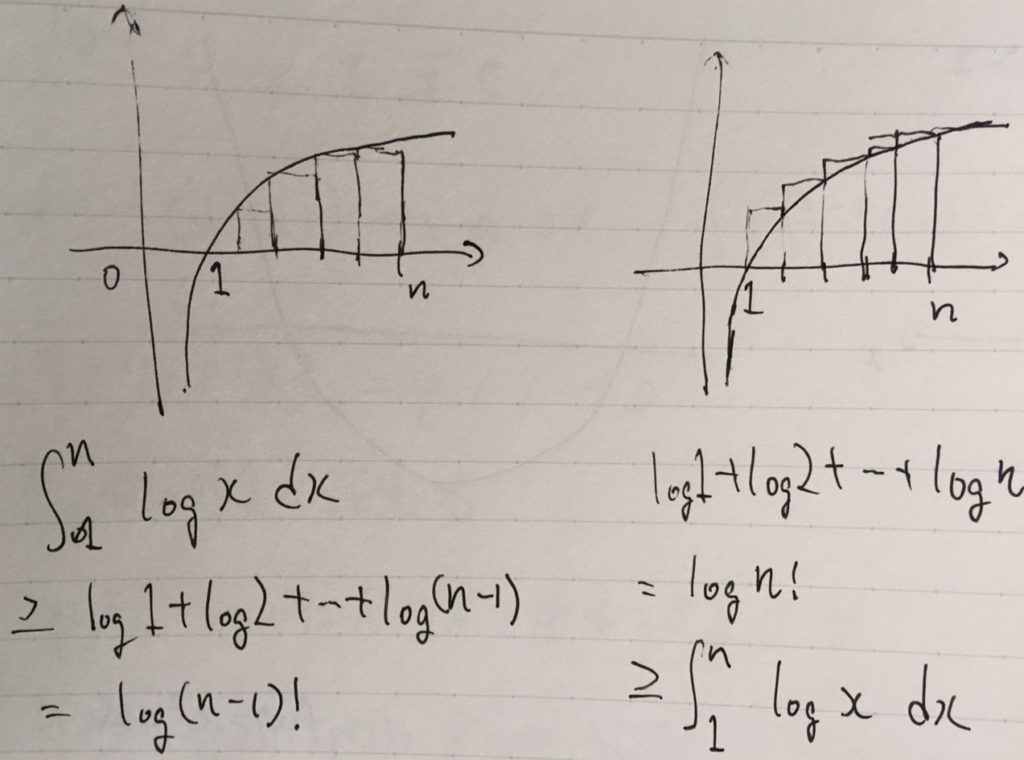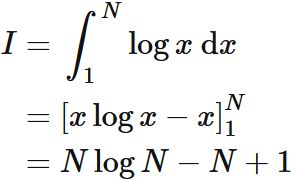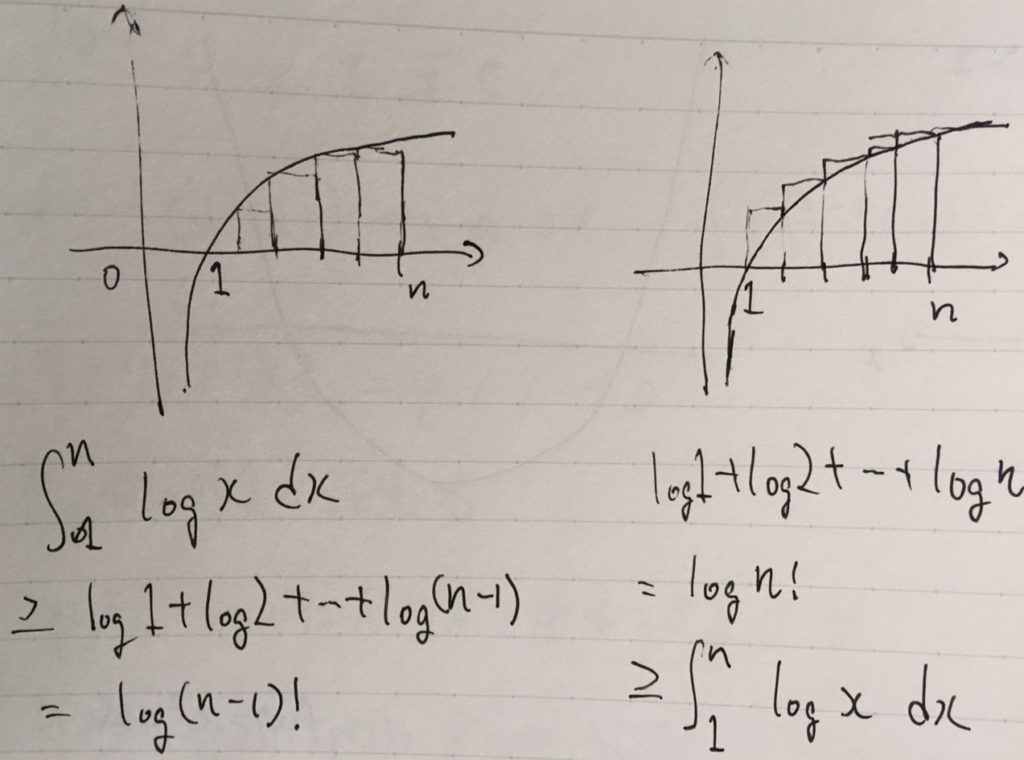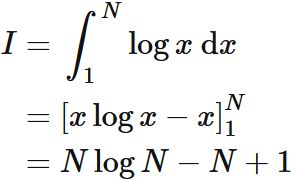スターリングの近似

スターリングの近似（英: Stirling's approximation）またはスターリングの公式（英: Stirling's formula）は、階乗、あるいはその拡張の一つであるガンマ関数の漸近近似である。名称は数学者ジェイムズ・スターリングにちなむ。

概要

スターリングの近似は精度に応じていくつかの形がある。応用上よく使われる形の公式は、ランダウの記号を用いて、

${\displaystyle \log n!=n\log n-n O(\log n)}$

である。O(log n) における次の項は (1/2)log 2πn である。故に、次によい近似の漸近公式は

${\displaystyle n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}}$

である。（ここで記号 ${\displaystyle \sim }$ は両辺の比が（n → ∞ のとき） 1 に収束することを意味する。）

n! の漸近近似よりもむしろ上下からの評価が必要なことがある。そのような評価として、任意の正の整数 n に対して

${\displaystyle {\sqrt {2\pi }}\,n^{n 1/2}e^{-n}\leq n!\leq en^{n 1/2}e^{-n}}$

が成り立ち、従って任意の n に対して比 n!/(n^{n 1/2}e⁻ⁿ) は √2π = 2.5066... と e = 2.71828... の間にある。

スターリングの近似は階乗の複素引数への拡張の一つであるガンマ関数 Γ(z)（正の整数 n に対し Γ(n) = (n − 1)! が成り立つ；ボーア・モレルップの定理も参照）に拡張することができ、

${\displaystyle \Gamma (z)\sim {\sqrt {\frac {2\pi }{z}}}\left({\frac {z}{e}}\right)^{z}\qquad (\vert \arg z\vert \leq \pi -\varepsilon ,\;\vert z\vert \to \infty )}$

が成り立つ（ただし ε > 0）。|arg z | → π のときは収束が遅くなるため、応用上は相補公式などを用いて |arg z | ≤ π/2 程度に制限することが多い。

導出

初等的な導出

スターリングの公式の厳密な証明にはオイラーの和公式、あるいは鞍点法といった複素解析の技法などを用いられることが多いが、初等的に導くことも可能である。まず階乗の対数を積分で近似する。logが凹関数であることから k-1

${\displaystyle \log k-(k-x)\{\log k-\log(k-1)\}\;<\;\log x\;<\;\log k-{\frac {1}{k}}(k-x)}$

これを k-1 から k まで積分して

${\displaystyle {\begin{aligned}&\log k-{\frac {1}{2}}\{\log k-\log(k-1)\}\;<\;\int _{k-1}^{k}\log x\,dx\;<\;\log k-{\frac {1}{2k}}\\&\int _{k-1}^{k}\log x\,dx {\frac {1}{2k}}\;<\;\log k\;<\;\int _{k-1}^{k}\log x\,dx {\frac {1}{2}}\{\log k-\log(k-1)\}\end{aligned}}}$

k=m 1,m 2,...,n に対して足し合わせると

${\displaystyle {\begin{aligned}\log {\frac {n!}{m!}}&=\sum _{k=m 1}^{n}\log k\\&>\int _{m}^{n}\log x\,dx \sum _{k=m 1}^{n}{\frac {1}{2k}}\\&>\int _{m}^{n}\log x\,dx {\frac {1}{2n}}-{\frac {1}{2m}} \int _{m}^{n}{\frac {1}{2x}}\,dx\\&=(n 1/2)\log n-n 1/(2n)-(m 1/2)\log m m-1/(2m)\\\log {\frac {n!}{m!}}&=\sum _{k=m 1}^{n}\log k\\&<\int _{m}^{n}\log x\,dx {\frac {1}{2}}\{\log n-\log m\}\\&=(n 1/2)\log n-n-(m 1/2)\log m m\end{aligned}}}$

${\displaystyle {\frac {n^{n 1/2}e^{-n 1/(2n)}}{m^{m 1/2}e^{-m 1/(2m)}}}<{\frac {n!}{m!}}<{\frac {n^{n 1/2}e^{-n}}{m^{m 1/2}e^{-m}}}}$

ここで ${\displaystyle \;a_{n}={\frac {n!}{n^{n 1/2}e^{-n}}}\;}$ と定めると

${\displaystyle {\frac {e^{1/(2n)}}{e^{1/(2m)}}}<{\frac {a_{n}}{a_{m}}}<1}$

m,n→∞のとき最左辺は1に収束するから、特に n=2m のとき

${\displaystyle \lim _{m\to \infty }{\frac {a_{2m}}{a_{m}}}=1}$

これとウォリスの公式の系 ${\displaystyle \;\lim _{n\to \infty }{\frac {4^{n}(n!)^{2}}{{\sqrt {n}}(2n)!}}={\sqrt {\pi }}\;}$ と比較すると、

${\displaystyle {\frac {4^{n}(n!)^{2}}{{\sqrt {n}}(2n)!}}={\frac {4^{n}(a_{n}n^{n 1/2}e^{-n})^{2}}{{\sqrt {n}}a_{2n}(2n)^{2n 1/2}e^{-2n}}}={\frac {a_{n}^{2}}{{\sqrt {2}}a_{2n}}}}$

${\displaystyle \lim _{n\to \infty }a_{n}=\lim _{n\to \infty }{\frac {4^{n}(n!)^{2}}{{\sqrt {n}}(2n)!}}{\frac {{\sqrt {2}}a_{2n}}{a_{n}}}={\sqrt {2\pi }}}$

を得る。

精度の改善

精度を改善するために a_n を評価する。

${\displaystyle {\begin{aligned}\log {\frac {a_{m}}{a_{m 1}}}&=\log m!-\left(m {\frac {1}{2}}\right)\log m m-\log(m 1)! \left(m {\frac {3}{2}}\right)\log(m 1)-m-1\\&=\left(m {\frac {1}{2}}\right)\log \left(1 {\frac {1}{m}}\right)-1\\&=\left(m {\frac {1}{2}}\right)\sum _{k=1}^{\infty }{\frac {(-1)^{k-1}}{k}}{\frac {1}{m^{k}}}-1\\&=\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{k 1}}{\frac {1}{m^{k}}} \sum _{k=1}^{\infty }{\frac {(-1)^{k-1}}{2k}}{\frac {1}{m^{k}}}-1\\&=\sum _{k=2}^{\infty }{\frac {(k-1)(-1)^{k}}{2k(k 1)}}{\frac {1}{m^{k}}}\end{aligned}}}$

${\displaystyle {\begin{aligned}\log {\frac {a_{n}}{\sqrt {2\pi }}}&=\sum _{m=n}^{\infty }\log {\frac {a_{m}}{a_{m 1}}}=\sum _{k=2}^{\infty }{\frac {(k-1)(-1)^{k}}{2k(k 1)}}\sum _{m=n}^{\infty }{\frac {1}{m^{k}}}\\&=\sum _{k=2}^{\infty }{\frac {(-1)^{k}}{2k(k 1)}}\left\{{\frac {1}{n^{k-1}}} O\left({\frac {1}{n^{k}}}\right)\right\}\\&={\frac {1}{12n}} O\left({\frac {1}{n^{2}}}\right)\end{aligned}}}$

従って

${\displaystyle n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\exp \left({\frac {1}{12n}}\right)}$

オイラーの和公式による導出

オイラーの乗積表示によるガンマ関数の定義の対数をとり

${\displaystyle {\begin{aligned}\log \Gamma (z)&=\log {\big \{}(z-1)\Gamma (z-1){\big \}}\\&=\lim _{N\to \infty }(z-1)\log N \sum _{n=1}^{N}{\big \{}\log n-\log(n z-1){\big \}}\end{aligned}}}$

${\displaystyle f(n)=\log n-\log(n z-1)}$ にオイラーの和公式を適用すれば

${\displaystyle {\begin{aligned}\log \Gamma (z)&=\lim _{N\to \infty }(z-1)\log N \int _{n=1}^{N}f(n)\,dn {\frac {1}{2}}{\big (}f(N) f(1){\big )}\\&\qquad \sum _{k=1}^{m}{\frac {B_{2k}}{(2k)!}}\left(f^{(2k-1)}(N)-f^{(2k-1)}(1)\right) \int _{n=1}^{N}{\frac {B_{2m 1}(n-\lfloor n\rfloor )}{(2m 1)!}}f^{(2m 1)}(n)\,dn\\&=\lim _{N\to \infty }(z-1)\log N {\bigg [}n\log n-n-(n z-1)\log(n z-1) (n z-1){\bigg ]}_{n=1}^{N} {\frac {1}{2}}{\big \{}\log N-\log(N z-1)-\log z{\big \}}\\&\qquad \sum _{k=1}^{m}{\frac {B_{2k}}{(2k)(2k-1)}}\left\{{\frac {1}{N^{2k-1}}}-{\frac {1}{(N z-1)^{2k-1}}}-1 {\frac {1}{z^{2k-1}}}\right\}\\&\qquad \int _{n=1}^{N}{\frac {B_{2m 1}(n-\lfloor n\rfloor )}{2m 1}}\left\{{\frac {1}{n^{2m 1}}}-{\frac {1}{(n z-1)^{2m 1}}}\right\}dn\\&=\lim _{N\to \infty }\left(N z-{\frac {1}{2}}\right){\big \{}\log N-\log(N z-1){\big \}} \left(z-{\frac {1}{2}}\right)\log z\\&\qquad \sum _{k=1}^{m}{\frac {B_{2k}}{(2k)(2k-1)}}\left\{{\frac {1}{N^{2k-1}}}-{\frac {1}{(N z-1)^{2k-1}}}-1 {\frac {1}{z^{2k-1}}}\right\}\\&\qquad \int _{n=1}^{N}{\frac {B_{2m 1}(n-\lfloor n\rfloor )}{2m 1}}\left\{{\frac {1}{n^{2m 1}}}-{\frac {1}{(n z-1)^{2m 1}}}\right\}dn\\&=-z 1 \left(z-{\frac {1}{2}}\right)\log z-\sum _{k=1}^{m}{\frac {B_{2k}}{(2k)(2k-1)}}\left(1-{\frac {1}{z^{2k-1}}}\right)\\&\qquad \int _{n=1}^{N}{\frac {B_{2m 1}(n-\lfloor n\rfloor )}{2m 1}}\left\{{\frac {1}{n^{2m 1}}}-{\frac {1}{(n z-1)^{2m 1}}}\right\}dn\end{aligned}}}$

となる。右辺の定数を集めて

${\displaystyle C=1-\sum _{k=1}^{m}{\frac {B_{2k}}{(2k)(2k-1)}} \int _{n=1}^{N}{\frac {B_{2m 1}(n-\lfloor n\rfloor )dn}{(2m 1)n^{2m 1}}}}$

とすれば

${\displaystyle \log \Gamma (z)=C-z \left(z-{\frac {1}{2}}\right)\log z \sum _{k=1}^{m}{\frac {B_{2k}}{(2k)(2k-1)z^{2k-1}}}-\int _{n=1}^{N}{\frac {B_{2m 1}(n-\lfloor n\rfloor )dn}{(2m 1)(n z-1)^{2m 1}}}}$

となり、この主要部をガンマ関数の相補公式に代入して ${\displaystyle z\to i\infty }$ とすれば

${\displaystyle \Gamma (z)\Gamma (1-z)=-z\Gamma (z)\Gamma (-z)={\frac {\pi }{\sin \pi z}}}$

${\displaystyle \pi i \log z \log \Gamma (z) \log \Gamma (-z)-\log \sin \pi z-\log \pi =0}$

${\displaystyle \pi i \log z C-z \left(z-{\frac {1}{2}}\right)\log z C z \left(-z-{\frac {1}{2}}\right)\left(\pi i \log z\right)-\log \sin \pi z-\log \pi =0}$

${\displaystyle 2C {\frac {\pi i}{2}}-\pi iz-\log \sin \pi z-\log \pi =0}$

となるが

${\displaystyle \log \sin \pi z=\log \left(e^{\pi iz}-e^{-\pi iz}\right)-{\frac {\pi i}{2}}-\log 2\sim \pi iz-{\frac {\pi i}{2}}-\log 2}$

であるから

${\displaystyle C={\frac {\log 2\pi }{2}}}$

を得る。剰余項については

${\displaystyle \alpha ={\frac {2}{1 \cos \arg z}}}$

として

${\displaystyle {\begin{aligned}\left|\int _{n=1}^{N}{\frac {B_{2m 1}(n-\lfloor n\rfloor )dn}{(2m 1)(n z-1)^{2m 1}}}\right|&\leq {\frac {\left|B_{2m}\right|}{2m}}\int _{n=1}^{N}{\frac {dn}{\left|n z-1\right|^{2m 1}}}\\&\leq {\frac {\left|B_{2m}\right|}{2m\alpha ^{2m 1}}}\int _{n=1}^{N}{\frac {dn}{(n \left|z\right|-1)^{2m 1}}}={\frac {\left|B_{2m}\right|}{\alpha ^{2m 1}\left|z\right|^{2m}}}=O\left(z^{-2m}\right)\\\end{aligned}}}$

である。故に

を得る。最初の数項を書き下せば

${\displaystyle \log \Gamma (z)\sim \log {\sqrt {2\pi }}-z \left(z-{\frac {1}{2}}\right)\log z {\frac {1}{12z}}-{\frac {1}{360z^{3}}} {\frac {1}{1260z^{5}}}-{\frac {1}{1680z^{7}}} {\frac {1}{1188z^{9}}}}$

${\displaystyle \Gamma (z)\sim {\sqrt {\frac {2\pi }{z}}}\left({\frac {z}{e}}\right)^{z}\exp \left({\frac {1}{12z}}-{\frac {1}{360z^{3}}} {\frac {1}{1260z^{5}}}-{\frac {1}{1680z^{7}}} {\frac {1}{1188z^{9}}}\right)}$

とやり、指数関数のテイラー展開により

${\displaystyle \Gamma (z)\sim {\sqrt {\frac {2\pi }{z}}}\left({\frac {z}{e}}\right)^{z}\left(1 {\frac {1}{12z}} {\frac {1}{288z^{2}}}-{\frac {139}{51840z^{3}}}\right)}$

となる。

鞍点法による導出

スターリングの公式は鞍点法の好適例とされることが多いが、実際に複素平面全体（負の実数を除く）で漸近近似が成立することを鞍点法によって示すのは困難であるから、ここでは ${\displaystyle z}$ を正の実数に限定する。ガンマ関数は ${\displaystyle t=z(1 u)}$ の置換により

${\displaystyle {\begin{aligned}\Gamma (z 1)&=\int _{0}^{\infty }t^{z}e^{-t}dt\\&=\int _{-1}^{\infty }z^{z}(1 u)^{z}e^{-z-zu}zdu\\&=z^{z 1}e^{-z}\int _{-1}^{\infty }e^{-z\left\{u-\log(1 u)\right\}}du\\&=z^{z 1}e^{-z}\left(\int _{-1}^{-\varepsilon }e^{-z\left\{u-\log(1 u)\right\}}du \int _{-\varepsilon }^{\varepsilon }{e^{-z\left\{u-\log(1 u)\right\}}du} \int _{\varepsilon }^{\infty }e^{-z\left\{u-\log(1 u)\right\}}du\right)\qquad (\varepsilon \ll 1)\\\end{aligned}}}$

となるが、${\displaystyle z}$ が十分に大きければ ${\displaystyle u=0}$ の付近が支配的であるから

${\displaystyle \Gamma (z 1)\approx z^{z 1}e^{-z}\int _{-\varepsilon }^{\varepsilon }e^{-z\left\{u-\log(1 u)\right\}}du\approx z^{z 1}e^{-z}\int _{-\varepsilon }^{\varepsilon }e^{-{\tfrac {zu^{2}}{2}}}du\approx z^{z 1}e^{-z}\int _{-\infty }^{\infty }e^{-{\tfrac {zu^{2}}{2}}}du}$

という近似が許され、ガウス積分により

${\displaystyle \Gamma (z 1)\sim z^{z 1}e^{-z}{\sqrt {\frac {2\pi }{z}}}={\sqrt {2\pi z}}\left({\frac {z}{e}}\right)^{z}}$

を得る。${\displaystyle \varepsilon =z^{-{\tfrac {1}{3}}}}$ として、近似の誤差は

${\displaystyle {\begin{aligned}\left|\int _{-1}^{-\varepsilon }e^{-z\left\{u-\log(1 u)\right\}}du\right|&\leq {\frac {1}{\varepsilon }}\int _{-1}^{-\varepsilon }\left|{\frac {-u}{(1 u)}}e^{-z\left\{u-\log(1 u)\right\}}\right|du={\frac {1}{\varepsilon z}}\left[e^{-z\left\{u-\log(1 u)\right\}}\right]_{-1}^{-\varepsilon }\\&={\frac {1}{\varepsilon z}}\left\{e^{-z\left({\tfrac {\varepsilon ^{2}}{2}} O(\varepsilon ^{3})\right)}\right\}-0\approx z^{\tfrac {2}{3}}e^{-{\tfrac {z^{1/3}}{2}}}\end{aligned}}}$

${\displaystyle {\begin{aligned}\left|\int _{\varepsilon }^{\infty }e^{-z\left\{u-\log(1 u)\right\}}du\right|&\leq {\frac {2}{\varepsilon }}\int _{\varepsilon }^{\infty }\left|{\frac {2u}{(1 u)\varepsilon }}e^{-z\left\{u-\log(1 u)\right\}}\right|du={\frac {2}{\varepsilon z}}\left[-e^{-z\left\{u-\log(1 u)\right\}}\right]_{\varepsilon }^{\infty }\\&=0-{\frac {2}{\varepsilon z}}\left\{e^{-z\left({\tfrac {\varepsilon ^{2}}{2}} O(\varepsilon ^{3})\right)}\right\}\approx 2z^{\tfrac {2}{3}}e^{-{\tfrac {z^{1/3}}{2}}}\end{aligned}}}$

${\displaystyle {\begin{aligned}\int _{-\varepsilon }^{\varepsilon }e^{-z\left\{u-\log(1 u)\right\}}du&=\int _{-\varepsilon }^{\varepsilon }e^{-z\left({\tfrac {u^{2}}{2}}-{\tfrac {u^{3}}{3}} O(u^{4})\right)}du=\int _{-\varepsilon }^{\varepsilon }e^{-{\tfrac {zu^{2}}{2}}}e^{z\left({\tfrac {u^{3}}{3}} O(u^{4})\right)}du\\&=\int _{-\varepsilon }^{\varepsilon }e^{-{\tfrac {zu^{2}}{2}}}\left(1 {\frac {zu^{3}}{3}} zO(u^{4})\right)du\\&=\int _{-\varepsilon }^{\varepsilon }e^{-{\tfrac {zu^{2}}{2}}}\left(1 zO(u^{4})\right)du\\\end{aligned}}}$

${\displaystyle \left|\int _{-\varepsilon }^{\varepsilon }e^{-z\left\{u-\log(1 u)\right\}}du-\int _{-\varepsilon }^{\varepsilon }e^{-{\tfrac {zu^{2}}{2}}}du\right|\leq \left|zO(\varepsilon ^{4})\int _{-\varepsilon }^{\varepsilon }e^{-{\tfrac {zu^{2}}{2}}}du\right|=\left|O(z^{-{\tfrac {1}{3}}})\int _{-\varepsilon }^{\varepsilon }e^{-{\tfrac {zu^{2}}{2}}}du\right|}$

であり

${\displaystyle z^{\tfrac {2}{3}}e^{-{\tfrac {z^{1/3}}{2}}}\ll z^{-{\tfrac {1}{2}}}\qquad (z\to \infty )}$

であるから

${\displaystyle \Gamma (z 1)={\sqrt {2\pi z}}\left({\frac {z}{e}}\right)^{z}\left(1 O(z^{-{\tfrac {1}{3}}})\right)}$

を得る。これは

${\displaystyle \lim _{z\to \infty }{\frac {\Gamma (z 1)}{{\sqrt {2\pi z}}\left({\frac {z}{e}}\right)^{z}}}=1\qquad (|\arg z|<\pi )}$

を示すに十分である。ただし、実際の誤差は ${\displaystyle O(z^{-1})}$ であるが、それを鞍点法で示すのは困難である。

収束の速度と誤差見積もり

より正確に記すと、次のようになる。

${\displaystyle n!={\sqrt {2\pi n}}\;\left({\frac {n}{e}}\right)^{n}e^{\lambda _{n}}}$

ここで

${\displaystyle {\frac {1}{12n 1}}<\lambda _{n}<{\frac {1}{12n}}.}$

スターリングの公式は以下の級数（スターリング級数）の近似（初項で打ち切ったもの）である。

${\displaystyle n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\left(1 {\frac {1}{12n}} {\frac {1}{288n^{2}}}-{\frac {139}{51840n^{3}}}-{\frac {571}{2488320n^{4}}} \cdots \right)}$

${\displaystyle n\to \infty }$ としたとき、省かれた級数はその最初の項とそれ以降が相殺するように漸近していく。これは漸近展開の一例である。

以下のような階乗の対数の漸近展開も「スターリング級数」と呼ぶ。

${\displaystyle \ln n!\sim n\ln n-n {\frac {1}{2}}\ln 2\pi n {\frac {1}{12n}}-{\frac {1}{360n^{3}}} {\frac {1}{1260n^{5}}}-{\frac {1}{1680n^{7}}} \cdots }$

この場合、誤差は打ち切った級数の初項と同じ符号で同程度の大きさであることが知られている。

ガンマ関数に対するスターリングの公式

すべての正の整数に対して、

${\displaystyle n!=\Pi (n)=\Gamma (n 1)}$

が成り立つ。ここで Γ はガンマ関数を表す。

しかしながら、パイ関数 ${\displaystyle \Pi (z)=\Gamma (z 1)}$ は、階乗とは異なり、より広く、正でない整数を除いてすべての複素数に対して定義される。それにもかかわらず、スターリングの公式をなお適用することができる。Re z > 0 であれば

${\displaystyle \log \Gamma (z)=\left(z-{\tfrac {1}{2}}\right)\log z-z {\tfrac {1}{2}}\log 2\pi 2\int _{0}^{\infty }{\frac {\arctan(t/z)}{e^{2\pi t}-1}}\,dt}$

が成り立つ。 部分積分を繰り返すことで次が得られる

${\displaystyle \log \Gamma (z)\sim \left(z-{\tfrac {1}{2}}\right)\log z-z {\tfrac {1}{2}}\log 2\pi \sum _{n=1}^{\infty }{\frac {B_{2n}}{2n(2n-1)z^{2n-1}}}.}$

ここで B_n は n 番目のベルヌーイ数である。（無限和は収束しないので、この公式は漸近展開にすぎないことに注意する。）公式はεを正数として |arg z| < π − ε であるときに絶対値の十分大きい z に対して成り立つ。公式の右辺に現れる級数はスターリング級数と呼ばれる。最初の m 項が使われるとき誤差項は ${\displaystyle O(z^{-2m-1})}$ である。対応する近似は

${\displaystyle \Gamma (z)={\sqrt {\frac {2\pi }{z}}}~{\left({\frac {z}{e}}\right)}^{z}\left(1 O\left({\frac {1}{z}}\right)\right)}$

のように書ける。この漸近展開のより進んだ応用は Re z が定数の複素変数 z に対してである。例えば直線 1/4 it 上でリーマン・ジーゲルテータ関数の Im z において適用されたスターリングの公式を見よ。

ビネーの公式

スターリングの公式は収束しない級数を伴うので解析的に扱いづらいが、収束しない級数を収束する積分に換えたものとしてビネーの(第二)公式がある。

${\displaystyle \Gamma (z 1)={\sqrt {2\pi z}}\left({\frac {z}{e}}\right)^{z}e^{\mu (z)},\quad \mu (z)=2\int _{0}^{\infty }{\frac {\arctan(t/z)}{e^{2\pi t}-1}}dt,\quad (\Re {z}>0)}$

ビネーの公式は、スターリングの級数を形式的に(収束条件を無視して)操作することによっても導かれるが、厳密には対数ガンマ関数の導関数にアーベル・プラナの和公式を適用して得られる。

${\displaystyle {\frac {d}{dz}}\log \Gamma (z)=\lim _{N\to \infty }\log N-\sum _{n=0}^{N}{\frac {1}{n z}}}$

${\displaystyle {\frac {d^{2}}{dz^{2}}}\log \Gamma (z)=\sum _{n=0}^{\infty }{\frac {1}{(n z)^{2}}}}$

${\displaystyle \Re z>0}$ なら ${\displaystyle f=(n z)^{-2}}$ は右半平面において正則であるからプラナの和公式により

${\displaystyle {\begin{aligned}{\frac {d^{2}}{dz^{2}}}\log \Gamma (z)&=\int _{0}^{\infty }{\frac {1}{(n z)^{2}}}dt {\frac {1}{2z^{2}}} i\int _{0}^{\infty }{\frac {(z it)^{-2}-(z-it)^{-2}}{e^{2\pi t}-1}}dt\\&={\frac {1}{z}} {\frac {1}{2z^{2}}} i\int _{0}^{\infty }{\frac {(z it)^{-2}-(z-it)^{-2}}{e^{2\pi t}-1}}dt\\\end{aligned}}}$

積分して

${\displaystyle {\frac {d}{dz}}\log \Gamma (z)=C_{1} \log z-{\frac {1}{2z}} i\int _{0}^{\infty }{\frac {-(z it)^{-1} (z-it)^{-1}}{e^{2\pi t}-1}}dt}$

${\displaystyle {\begin{aligned}\log \Gamma (z)&=C_{2} C_{1}z z\log z-{\frac {\log z}{2}} i\int _{0}^{\infty }{\frac {-\log(z it) \log(z-it)}{e^{2\pi t}-1}}dt\\&=C_{2} C_{1}z \left(z-{\frac {1}{2}}\right)\log z 2\int _{0}^{\infty }{\frac {\arctan(t/z)}{e^{2\pi t}-1}}dt\\\end{aligned}}}$

${\displaystyle \Re z>0}$ なら${\displaystyle |\tan(t/z)|$ は有界であるから

${\displaystyle {\begin{aligned}\left|\int _{0}^{\infty }{\frac {\arctan(t/z)}{e^{2\pi t}-1}}dt\right|&\leq \left|\int _{0}^{|z|^{1/2}}{\frac {\arctan(t/z)}{e^{2\pi t}-1}}dt\right| \left|\int _{|z|^{1/2}}^{\infty }{\frac {\arctan(t/z)}{e^{2\pi t}-1}}dt\right|\\&\leq \int _{0}^{|z|^{1/2}}{\frac {\sum _{k=1}^{\infty }|t/z|^{k}dt}{2\pi t}} M\int _{|z|^{1/2}}^{\infty }{\frac {e^{2\pi }dt}{(e^{2\pi }-1)e^{t}e^{2\pi }}}\qquad (|z|>1)\\&\leq \int _{0}^{|z|^{1/2}}{\frac {dt}{2\pi (|z|-t)}} {\frac {Me^{2\pi }}{e^{2\pi }-1}}\int _{t=|z|^{1/2}}^{\infty }e^{-2\pi t}dt\end{aligned}}}$

${\displaystyle \lim _{z\to \infty }\left|\int _{0}^{\infty }{\frac {\arctan(t/z)}{e^{2\pi t}-1}}dt\right|\leq \lim _{z\to \infty }{\frac {1}{2\pi }}{\Big [}\log \left(|z|-t\right){\Big ]}_{0}^{|z|^{1/2}} \lim _{z\to \infty }{\frac {Me^{2\pi }}{2\pi \left(e^{2\pi }-1\right)}}{\Big [}-e^{-2\pi t}{\Big ]}_{|z|^{1/2}}^{\infty }=0}$

である。 スターリングの公式と比較して積分定数を求め

${\displaystyle \log \Gamma (z)={\frac {1}{2}}\log 2\pi -z \left(z-{\frac {1}{2}}\right)\log z 2\int _{0}^{\infty }{\frac {\arctan(t/z)}{e^{2\pi t}-1}}dt}$

真数に直して

${\displaystyle \Gamma (z 1)=z\Gamma (z)={\sqrt {2\pi z}}\left({\frac {z}{e}}\right)^{z}e^{\mu (z)},\quad \mu (z)=2\int _{0}^{\infty }{\frac {\arctan(t/z)}{e^{2\pi t}-1}}dt,\quad (\Re z>0)}$

を得る。なお、ビネーの公式を元にして部分積分を繰り返すとスターリングの級数が得られる。

収束級数形式のスターリングの公式

トーマス・ベイズの John Canton への書簡が1763年に王立協会により公表されている。それによると、スターリングの公式は収束級数ではないとされていた。

スターリングの公式の収束級数形式を得るには以下を評価する。

${\displaystyle \int _{0}^{\infty }{\frac {2\arctan(t/z)}{\exp 2\pi t-1}}\,dt=\ln \Gamma (z)-\left(z-{\frac {1}{2}}\right)\ln z z-{\frac {1}{2}}\ln 2\pi }$

一つの方法として、階乗冪の逆数の収束級数を使う方法がある。${\displaystyle z^{\overline {n}}=z(z 1)\cdots (z n-1)}$ としたとき、次のようになる。

${\displaystyle \int _{0}^{\infty }{\frac {2\arctan(t/z)}{\exp 2\pi t-1}}\,dt=\sum _{n=1}^{\infty }{\frac {c_{n}}{(z 1)^{\overline {n}}}}}$

ここで

${\displaystyle c_{n}={\frac {1}{n}}\int _{0}^{1}x^{\overline {n}}\left(x-{\frac {1}{2}}\right)\,dx}$

である。以上から次のようなスターリング級数が得られる。

${\displaystyle {\begin{aligned}\ln \Gamma (z)&=\left(z-{\frac {1}{2}}\right)\ln z-z {\frac {1}{2}}\ln 2\pi \\&\quad {\frac {1}{12(z 1)}} {\frac {1}{12(z 1)(z 2)}} {\frac {59}{360(z 1)(z 2)(z 3)}} {\frac {29}{60(z 1)(z 2)(z 3)(z 4)}} \cdots \end{aligned}}}$

これは、${\displaystyle \Re z>0}$ のとき収束する。

計算機向けの変形

ガンマ関数の（関数電卓などの）計算機向けの近似として次の式がある。

${\displaystyle \Gamma (z)\sim {\sqrt {\frac {2\pi }{z}}}\left({\frac {z}{e}}{\sqrt {z\sinh {\frac {1}{z}} {\frac {1}{810z^{6}}}}}\right)^{z}}$

これは、次と同等である。

${\displaystyle 2\ln \Gamma (z)\sim \ln 2\pi -\ln z z\left\{2\ln z \ln \left(z\sinh {\frac {1}{z}} {\frac {1}{810z^{6}}}\right)-2\right\}}$

これらはスターリングの公式を組み替えて、その結果生じる冪級数と双曲線正弦関数のテイラー展開の間の合致を観察することで得られる。この近似は z の実数部が 8 以上のとき、小数点以下 8 桁を超える精度を持つ。2002年、Robert H. Windschitl がリソースの制限された計算機（電卓など）でのそれなりの正確性を持った近似としてこれを示した。

Gergő Nemes は 2007年にほぼ同程度の結果を与える近似式を提案した。こちらはより単純である。

${\displaystyle \Gamma (z)\sim {\sqrt {\frac {2\pi }{z}}}\left\{{\frac {1}{e}}\left(z {\frac {1}{12z-{\frac {1}{10z}}}}\right)\right\}^{z}}$

これは、次と同等である。

${\displaystyle \ln \Gamma (z)\sim {\frac {1}{2}}\left(\ln 2\pi -\ln z\right) z\left\{\ln \left(z {\frac {1}{12z-{\frac {1}{10z}}}}\right)-1\right\}}$

歴史

この公式は最初に次の形でアブラーム・ド・モアブルにより1730年に発見された。

${\displaystyle n!\sim [{\rm {constant}}]\cdot n^{n {\tfrac {1}{2}}}e^{-n}}$

スターリングの貢献は定数が ${\displaystyle {\sqrt {2\pi }}}$ であることを示したことである。より正確な形式はジャック・ビネが見出した。

スターリングの近似の「一次」バージョン ${\displaystyle n!=n^{n}}$ は、マックス・プランクが1901年の黒体放射の論文で使用した。これは多量の光子や振動子についての黒体放射エネルギーの方程式にリンクしている。この近似は量子論でよく使われ、例えばピーター・デバイとルイ・ド・ブロイも使っている。アルベルト・アインシュタインとサティエンドラ・ボースは違う方式を採用した。非常に大きな n について確率分布をグラフに描画してみると、両者はほぼ平行になる。

脚注

参考文献

• Abramowitz, Milton; Stegun, Irene A. (1964). Handbook of mathematical functions with formulas, graphs, and mathematical tables. National Bureau of Standards Applied Mathematics Series. 55. MR0167642. Zbl 0171.38503. http://www.math.hkbu.edu.hk/support/aands/toc.htm 
• Andrews, George E.; Askey, Richard; Roy, Ranjan (1999). Special functions. Encyclopedia of Mathematics and its Applications. 71. Cambridge University Press. ISBN 0-521-62321-9. MR1688958. Zbl 0920.33001. https://books.google.co.jp/books?id=kGshpCa3eYwC&pg=PA18. "1.4 Stirling's Asymptotic Formula" 
• Paris, R. B., and Kaminsky, D., Asymptotics and the Mellin-Barnes Integrals, Cambridge University Press, 2001
• Whittaker, E. T.; Watson, G. N. (1996). A course of modern analysis (Reprint of the fourth ed.). ISBN 0-521-58807-3. MR1424469. Zbl 0951.30002. https://books.google.co.jp/books?id=ULVdGZmi9VcC 

関連項目

• ランチョス近似

外部リンク

• スターリングの公式（漸近近似）の導出
• Elic W. Weisstein, Stirling's Approximation at MathWorld
• A collected derivation of Stirling's equation by Timothy Jones