パドヴァン数列

パドヴァン数列は、漸化式 ${\displaystyle a_{0}=a_{1}=a_{2}=1,\,a_{n}=a_{n-2} a_{n-3}}$ で表される数列である。

第0～25項（4桁未満）の値は次のとおりである：

1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265, 351, 465, 616, 816, ... （オンライン整数列大辞典の数列 A000931）

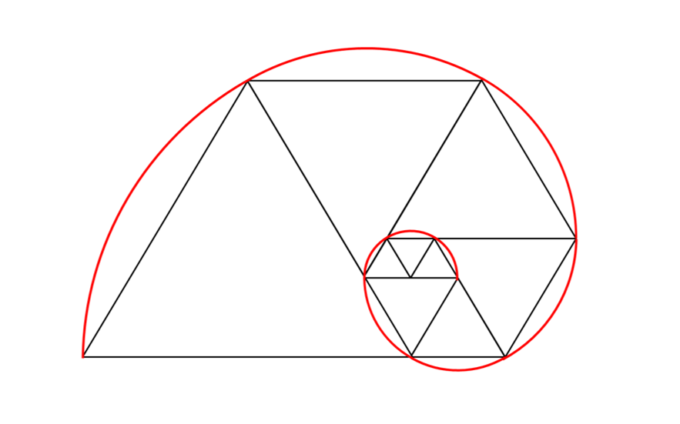
この、各項が2つ前と3つ前の項の和で与えられる数列は、イタリアの建築家リチャード・パドヴァンにちなんでパドヴァン数列と呼ばれている。

性質

• パドヴァン数列の母関数は次のとおりとなる：

${\displaystyle G(a_{n};x)={\frac {1 x}{1-x^{2}-x^{3}}}}$

• 別途、${\displaystyle n\geq 5}$ である各項は1つ前と5つ前の項の和としても与えられる。すなわち、

${\displaystyle a_{n}=a_{n-1} a_{n-5}}$

• ペラン数 ${\displaystyle p_{n}}$ とは、次の関係にある：

${\displaystyle p_{n}=a_{n 1} a_{n-10}}$

• 特性方程式：

${\displaystyle x^{3}-x-1=0}$

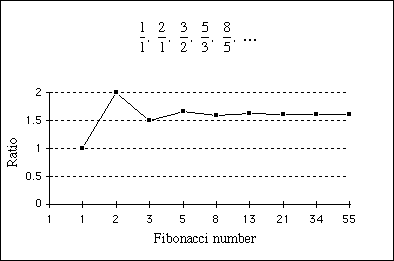
の唯一の実数解より、パドヴァン数列（ペラン数列も然り）の連続する2項の比の値はプラスチック数

${\displaystyle \rho ={\sqrt[{3}]{\frac {9 {\sqrt {69}}}{18}}} {\sqrt[{3}]{\frac {9-{\sqrt {69}}}{18}}}=1.324717957244746025960908854\cdots }$

に次第に近づくことになる。

脚注

外部リンク

• Weisstein, Eric W. "Padovan Sequence". mathworld.wolfram.com (英語).