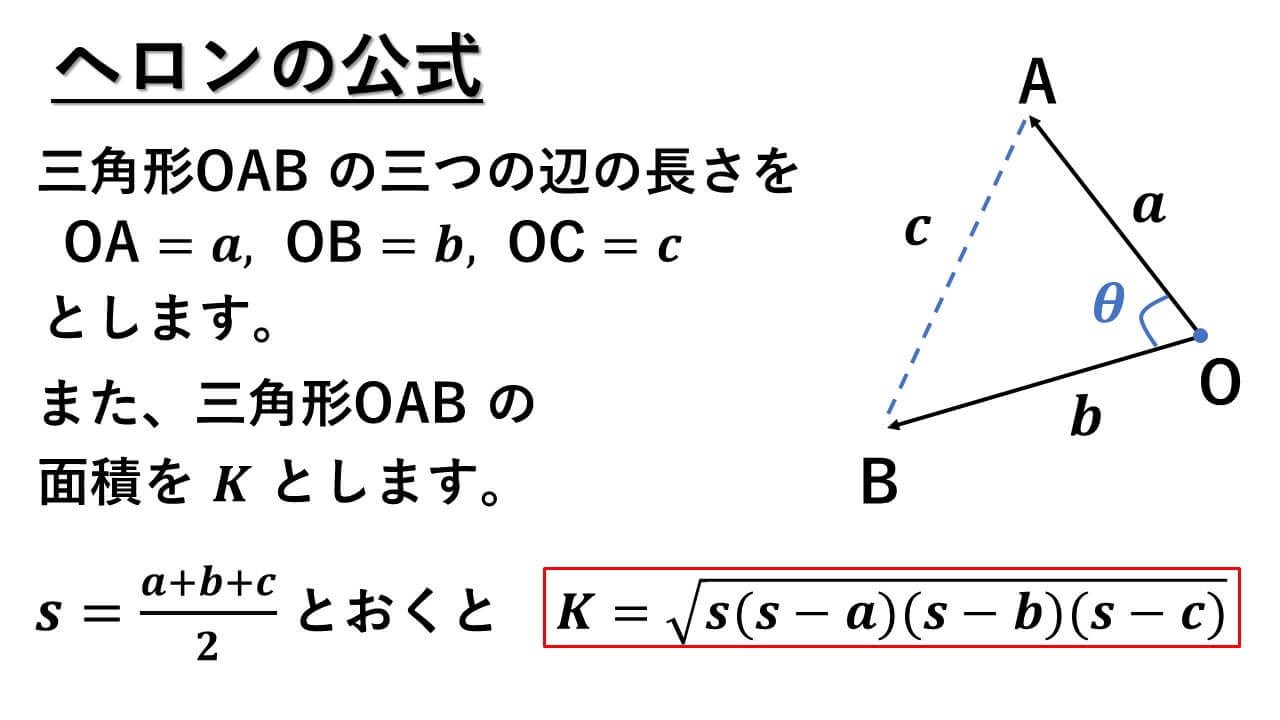
ヘロンの公式

ヘロンの公式（ヘロンのこうしき、英: Heron's formula, Hero's formula）とは、3辺の長さが a, b, c などと分かっている三角形の面積 S を求める公式のことである。

アレクサンドリアのヘロンが彼の著書『Metrica』の中で証明を与えていることから彼に帰せられる。

概要

この公式はアレクサンドリアのヘロンが彼の著書『Metrica』の中で証明を与えていることから彼に帰せられるが、現代ではこれ自体はシラクサのアルキメデスにも既知であったと考えられていて、さらにそれ以前から知られていた可能性もある。

一般化として、円に内接する四角形の面積を辺の長さから求めるブラーマグプタの公式があり、さらには円に内接するという条件を外し、角度も用いて四角形の面積を求めるブレートシュナイダーの公式がある。ヘロンの公式はこれらの公式の特別な場合となっている。

しかし、円に内接するn角形について面積を、その辺の長さから四則演算とk乗根をとる操作によって求める代数的な公式は n ≥ 5 では存在しないことが知られている。

公式

また、以下のような s を用いない表記もある。

${\displaystyle S={\frac {\sqrt {(a b c)(-a b c)(a-b c)(a b-c)}}{4}}}$

${\displaystyle S={\frac {\sqrt {2(a^{2}b^{2} a^{2}c^{2} b^{2}c^{2})-(a^{4} b^{4} c^{4})}}{4}}}$

${\displaystyle S={\frac {\sqrt {(a^{2} b^{2} c^{2})^{2}-2(a^{4} b^{4} c^{4})}}{4}}}$

${\displaystyle S={\frac {\sqrt {4b^{2}c^{2}-(a^{2}-b^{2}-c^{2})^{2}}}{4}}}$

特に下3つは一辺の長さが有理数の平方根であるときに有用である。

例

△ABCの3辺の長さを ${\displaystyle a,}$ ${\displaystyle b,}$ ${\displaystyle c}$ とし、面積を ${\displaystyle S}$ とする。 ${\displaystyle a=14,}$ ${\displaystyle b=13,}$ ${\displaystyle c=15}$ であるとき、

${\displaystyle s=}$ ${\displaystyle {\frac {a b c}{2}}=}$${\displaystyle {\frac {14 13 15}{2}}=21}$

よって、面積 ${\displaystyle S}$ は

${\displaystyle {\begin{aligned}S&={\sqrt {s(s-a)(s-b)(s-c)}}={\sqrt {21\cdot (21-14)\cdot (21-13)\cdot (21-15)}}\\&={\sqrt {21\cdot 7\cdot 8\cdot 6}}=84\end{aligned}}}$

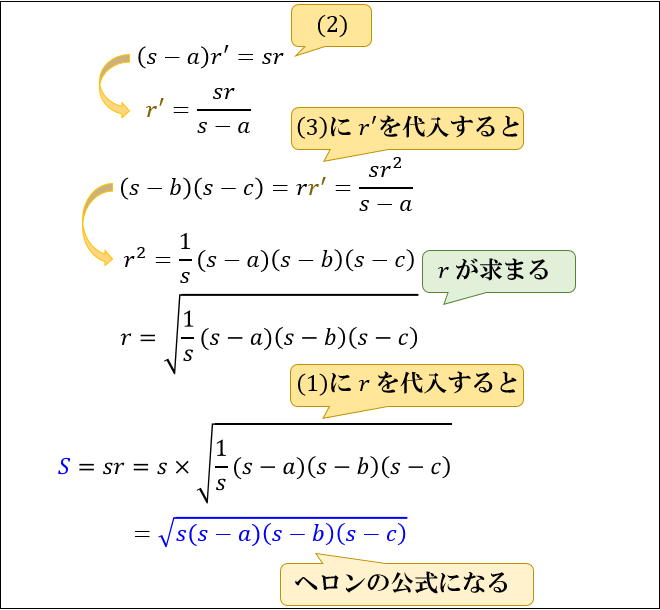
証明

三角関数を用いた証明

三角比、余弦定理、因数分解を用いた証明。

△ABC において、A, B, C の対辺 BC, CA, AB の長さをそれぞれ a, b, c とし、A から辺 BC に下ろした垂線の長さを h とする。

このとき△ABCの面積 S は、

${\displaystyle {\begin{aligned}S&={\frac {ah}{2}}={\frac {ab}{2}}\sin C={\frac {ab}{2}}{\sqrt {1-\cos ^{2}C}}\\&={\frac {ab}{2}}{\sqrt {(1 \cos C)(1-\cos C)}}\\&={\frac {ab}{2}}{\sqrt {\left(1 {\frac {a^{2} b^{2}-c^{2}}{2ab}}\right)\left(1-{\frac {a^{2} b^{2}-c^{2}}{2ab}}\right)}}\\&={\frac {ab}{2}}{\sqrt {{\frac {a^{2} 2ab b^{2}-c^{2}}{2ab}}\cdot {\frac {-(a^{2}-2ab b^{2}-c^{2})}{2ab}}}}\\&={\sqrt {{\frac {(a b)^{2}-c^{2}}{4}}\cdot {\frac {-[(a-b)^{2}-c^{2}]}{4}}}}\\&={\sqrt {{\frac {(a b c)(a b-c)}{4}}\cdot {\frac {-(a-b c)(a-b-c)}{4}}}}\\&={\sqrt {{\frac {a b c}{2}}\cdot {\frac {-a b c}{2}}\cdot {\frac {a-b c}{2}}\cdot {\frac {a b-c}{2}}}}\\&={\sqrt {{\frac {a b c}{2}}\left({\frac {a b c}{2}}-a\right)\left({\frac {a b c}{2}}-b\right)\left({\frac {a b c}{2}}-c\right)}}\end{aligned}}}$

となる。ここで、

${\displaystyle {\frac {a b c}{2}}=s}$

とおくと、

${\displaystyle S={\sqrt {s(s-a)(s-b)(s-c)}}}$

が得られる。

ピタゴラスの定理を用いた代数的証明

△ABC において、A, B, C の対辺 BC, CA, AB の長さをそれぞれ a, b, c とし、A から辺 BC に下ろした垂線 AH の長さを h とする。

この時△ABC の面積を S とすると h は、

${\displaystyle {{\text{1}} \over {\text{2}}}ah=S}$

なので、

${\displaystyle h={2S \over a}}$ (1)

と表せる。

適当な符号で、

${\displaystyle \pm {\text{CH}}\pm {\text{BH}}=a}$ (2)

は自明であり、

（±は鈍角三角形と鋭角三角形の場合分けを省くためである。）

ピタゴラスの定理より、

${\displaystyle {\text{CH}}={\sqrt {b^{2}-h^{2}}}}$ (3)

${\displaystyle {\text{BH}}={\sqrt {c^{2}-h^{2}}}}$ (4)

と表せるので、(3)(4)の式に(1)を代入し、(2)の式に(3)(4)を代入すると、

${\displaystyle \pm {\sqrt {b^{2}-\left({\frac {2S}{a}}\right)^{2}}}\pm {\sqrt {c^{2}-\left({\frac {2S}{a}}\right)^{2}}}=a}$

となる。

この式を S について解いた正の方が解である。

ピタゴラスの定理より、

${\displaystyle {\text{CH}}={\sqrt {b^{2}-h^{2}}}=a-d}$ (3)

${\displaystyle {\text{BH}}={\sqrt {c^{2}-h^{2}}}=d}$ (4)

と表すと、

${\displaystyle c^{2}=d^{2} h^{2}}$ (5)

${\displaystyle b^{2}=h^{2} (a-d)^{2}=h^{2} a^{2}-2ad d^{2}}$(6)

(5)の式を(6)の式に代入して、hを消すと、

${\displaystyle b^{2}=a^{2}-2ad c^{2}}$

${\displaystyle d={\frac {a^{2}-b^{2} c^{2}}{2a}}}$(7)

(7)の式を(5)の式に代入して、

${\displaystyle {\begin{aligned}h^{2}&=c^{2}-\left({\frac {a^{2}-b^{2} c^{2}}{2a}}\right)^{2}\\&={\frac {4a^{2}c^{2}-(a^{2}-b^{2} c^{2})^{2}}{4a^{2}}}\\&={\frac {(2ac)^{2}-(a^{2}-b^{2} c^{2})^{2}}{4a^{2}}}\\&={\frac {(2ac a^{2}-b^{2} c^{2})(2ac-a^{2} b^{2}-c^{2})}{4a^{2}}}\\&={\frac {((a c)^{2}-b^{2})(b^{2}-(a-c)^{2})}{4a^{2}}}\\&={\frac {(a b c)(a-b c)(a b-c)(-a b c)}{4a^{2}}}\\&={\frac {(a b c)(a b c-2b)(a b c-2c)(a b c-2a)}{4a^{2}}}\\\end{aligned}}}$

ここで ${\displaystyle a b c=T}$ とおくと、

${\displaystyle {\begin{aligned}h^{2}&={\frac {T(T-2b)(T-2c)(T-2a)}{4a^{2}}}\end{aligned}}}$

ここで ${\displaystyle s={\frac {a b c}{2}}}$ とおくと、 ${\displaystyle T=2s}$ となり、

${\displaystyle {\begin{aligned}h^{2}&={\frac {2s(2s-2b)(2s-2c)(2s-2a)}{4a^{2}}}\\&={\frac {16s(s-a)(s-b)(s-c)}{4a^{2}}}\end{aligned}}}$

${\displaystyle {\begin{aligned}h&={\frac {2{\sqrt {s(s-a)(s-b)(s-c)}}}{a}}\end{aligned}}}$

よって

${\displaystyle {\begin{aligned}S&={{\text{1}} \over {\text{2}}}ah\\&={{\text{1}} \over {\text{2}}}a{\frac {2{\sqrt {s(s-a)(s-b)(s-c)}}}{a}}\\&={\sqrt {s(s-a)(s-b)(s-c)}}\end{aligned}}}$

が得られる。

3次元版

ヘロンの公式の3次元版として、四面体の体積を6辺の長さから求める公式を紹介する。

n次元版

ヘロンの公式のn次元版はCayley-Menger Determinantとして知られている。

脚注

参考文献

• T・L・ヒース著、平田寛他訳『ギリシア数学史』共立出版、1998年5月。ISBN 4-320-01588-6

関連項目

外部リンク

• 『ヘロンの公式』 - コトバンク
• 『ヘロンの公式の証明と使用例』 - 高校数学の美しい物語
• Weisstein, Eric W. "Heron's Formula". mathworld.wolfram.com (英語).